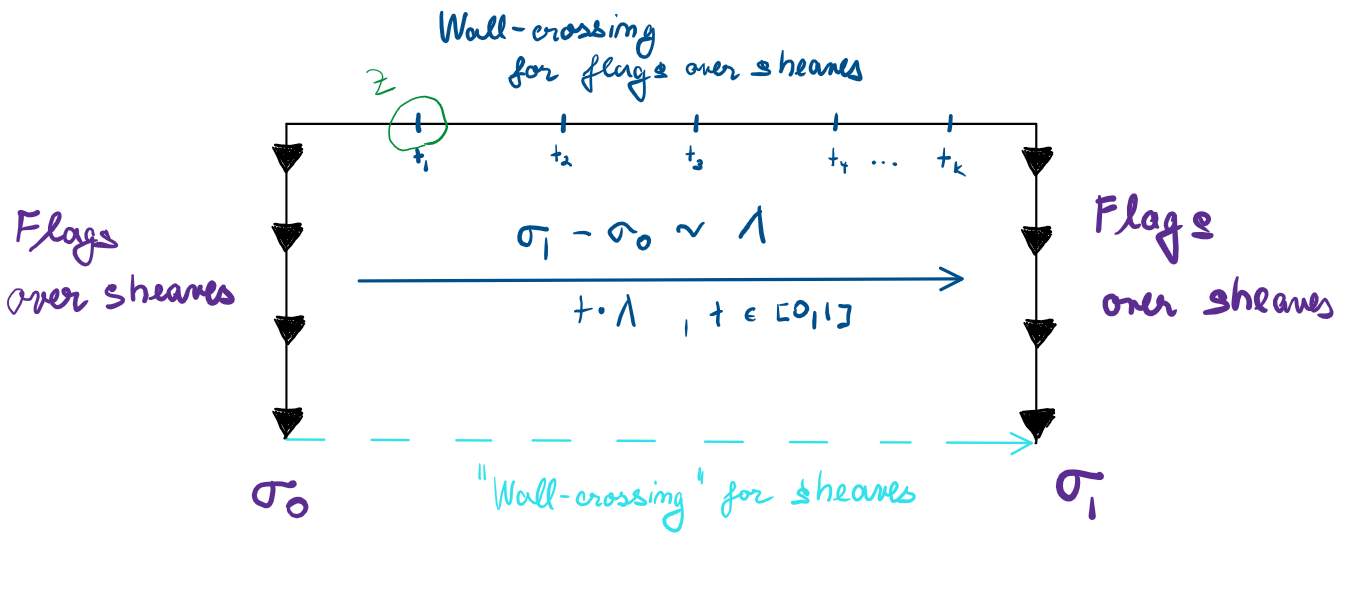Project 1

Proving wall-crossing for Calabi–Yau fourfolds

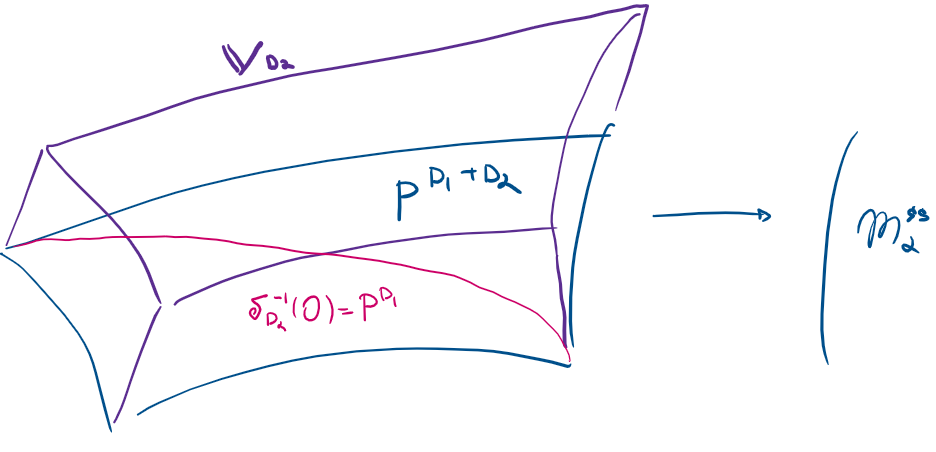
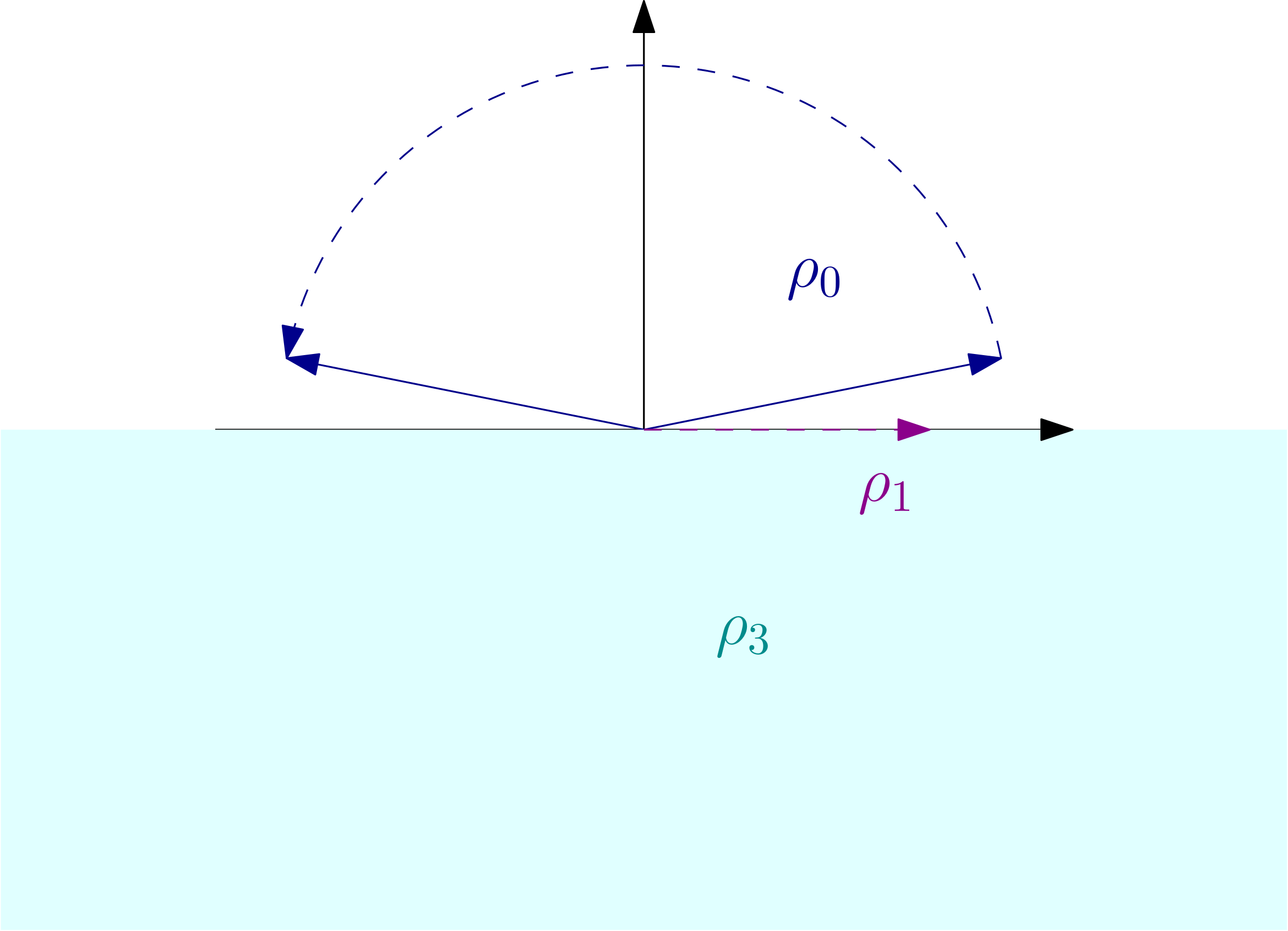
In this vast project, I have chosen to tackle the question of wall-crossing formulae for Calabi-Yau fourfolds which were originally conjecture by Gross-Joyce-Tanaka. A big part part of this project focused on making the result accessible and suitable for many applications. Another more technical part needed to address the problem of constructing appropriate obstruction theories on master spaces appearing in the argument. This second part will be addressed partially in my first paper on the topic while a completely general statement will be provided in a joint work with Kuhn and Thimm. Originally, I believed to have had a proof that the obstruction to the existence of such obstruction theories vanishes, but alas, I found an inconsistency. With Nick and Felix, we will work around this issue.

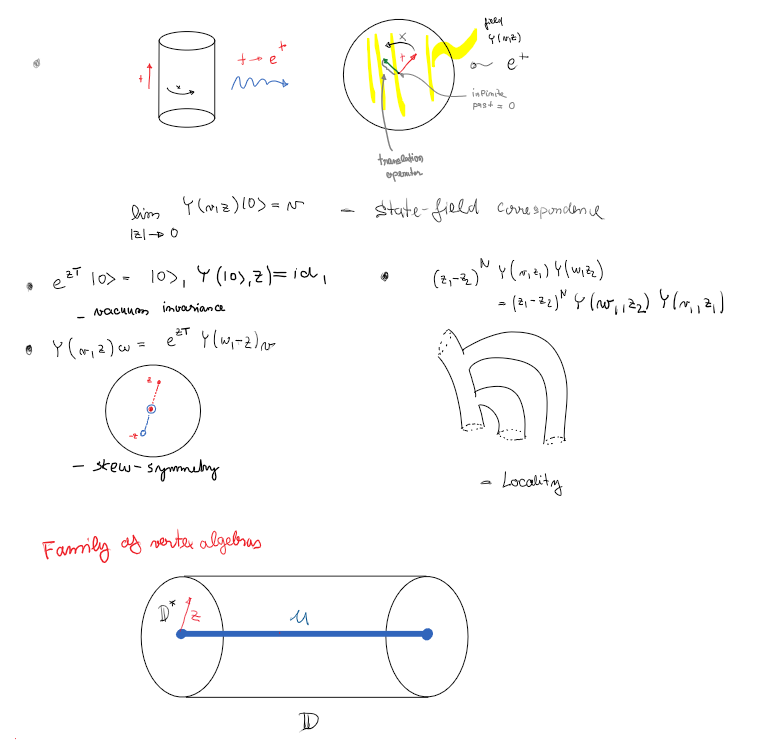
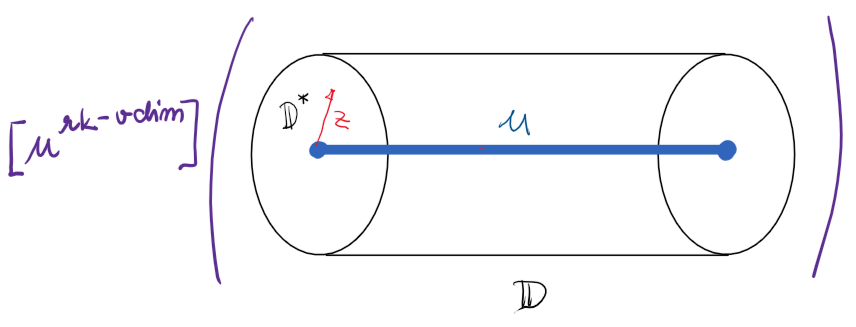
One of the interesting outcomes of my research is that one can wall-cross with some nice invariants obtained from multiplicative insertions. This refines the original formulation of Gross-Joyce-Tanaka who only dealt with full virtual fundamental classes. The geometric set up of such wall-crossing gives naturally rise to a representation theoretic structure I called additive formal families of vertex algebras. I will use this theory to prove multiple existing conjectures in the literature related to point and curve counting together with the results in Project 3.

I use formal families of vertex algebras in a formal variable u to formulate wall-crossing of invariants. The first picture represents a physical perspective of the origin of such families. To obtain explicit formulae, one takes an appropriate coefficient of the expansion in $u$ as is portrayed in the second illustration.
The proof is intricate as one first needs to construct self-dual obstruction theories for Mochizuki's enhanced master spaces represented on the left. The proof sketched in the diagram on the right requires many compatibilities between these obstruction theories which in general are violated.
On the left is represented the argument that proves that the produced invariants counting semistable torsion-free sheaves are well-defined. The second picture is one of the main applications of my work which has implications to 3-fold DT/PT correspondence. The figure represents the need to work with new families of stability conditions. In the third work in the series, I will therefore formulate the wall-crossing set up in terms of some generalizations of Bridgeland stability conditions.

References