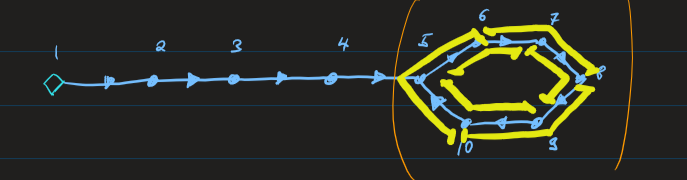
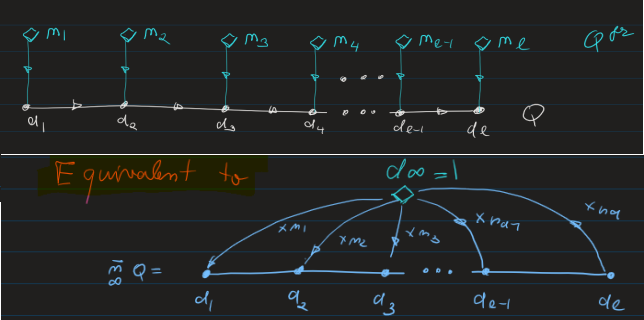
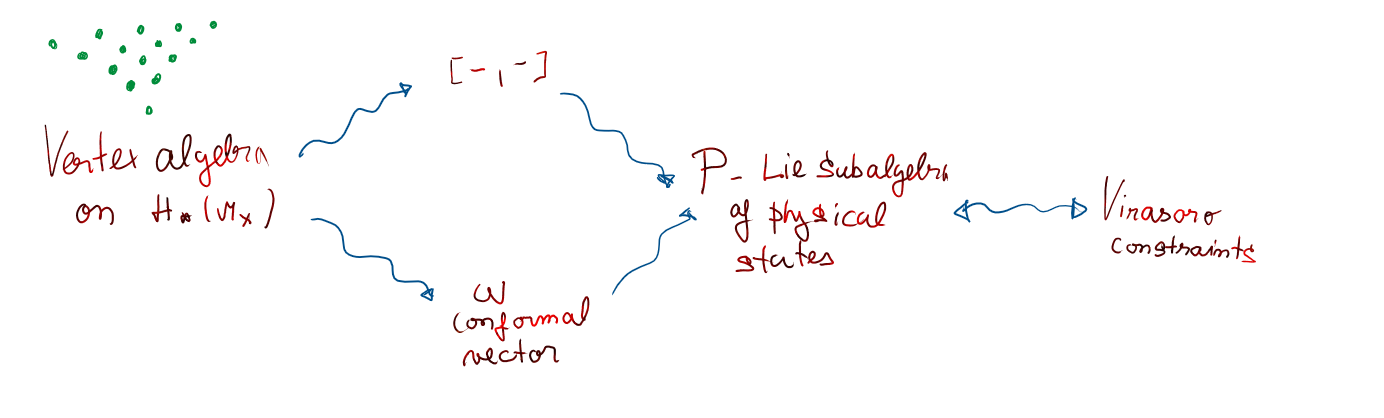
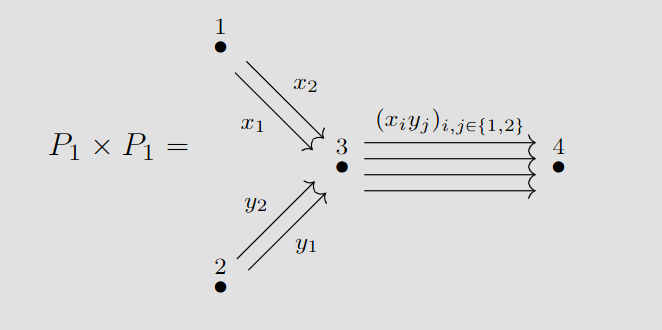
Project 2 | Arkadij Bojko

Following our success in pdf where I, Woonam Lim, and Miguel Moreira proved Virasoro constraints for moduli schemes of sheaves on curves and surfaces, I continue studying further settings where they may be present. The idea is to compare the constraints to the virtual fundamental class being a physical state of a geometrically constructed vertex algebra. This vertex algebra was introduced by Joyce to describe wall-crossing of sheaf-counting invariants. Consequently, Virasoro constraints are preserved by wall-crossing under changing stability conditions which can be also used to prove them for (framed) representations of quivers with relations as I do in my more recent work. A particularly enticing outcome of this work is the proof of sheaf-theoretic Virasoro constraints for $\mathbb{P}^2$ and $\mathbb{P}^1\times \mathbb{P}^1$ which are the main stepping stones to an independent proof for any surface due to an existing universality argument. This answers one of the fundamental questions of the subject - sheaf-theoretic Virasoro constraints for surfaces can be proved independently of GW theory.

A quiver with a cycle but with relations that still allow me to study its Virasoro constraints. On the right is the procedure of forming an auxiliary quiver that is used for constructing conformal elements and studying framed representations.

The sketch of the idea of the proof.

Here are the two quivers that are derived equivalent to $\mathbb{P}^2$ and $\mathbb{P}^1\times\mathbb{P}^1$ respectively. Proving Virasoro constraints for the quiver representations amounts to proving Virasoro constraints for sheaves.