Project 3
Wall-crossing for pair counting theories on Calabi--Yau fourfolds
Project 1 will provide tools for proving natural DT/PT correspondences on projective Calabi–Yau fourfolds. More interestingly still, I will address multiple conjectures postulated by Bae–Kool–Park about CY4 surface counting invariants. For elliptic fibrations, these results are closely related to DT/PT correspondencences on the base by the work of BKP.
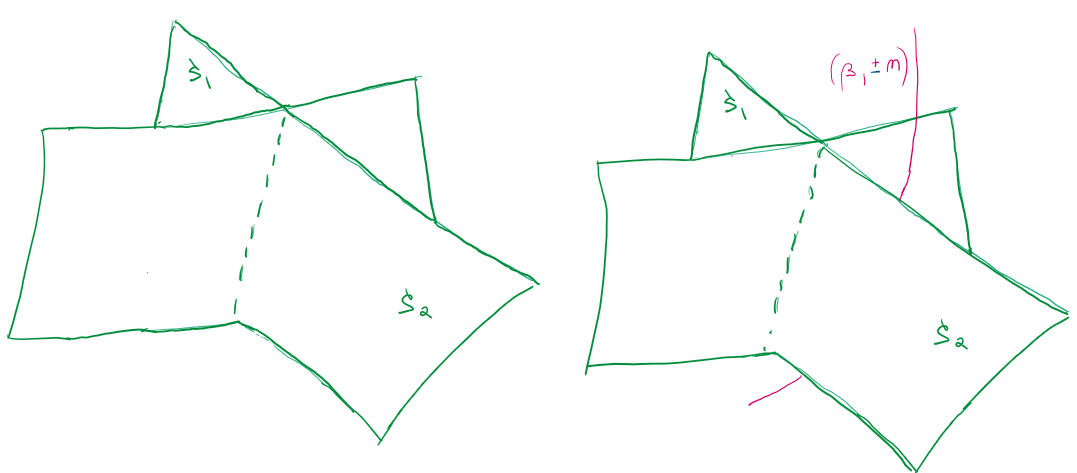
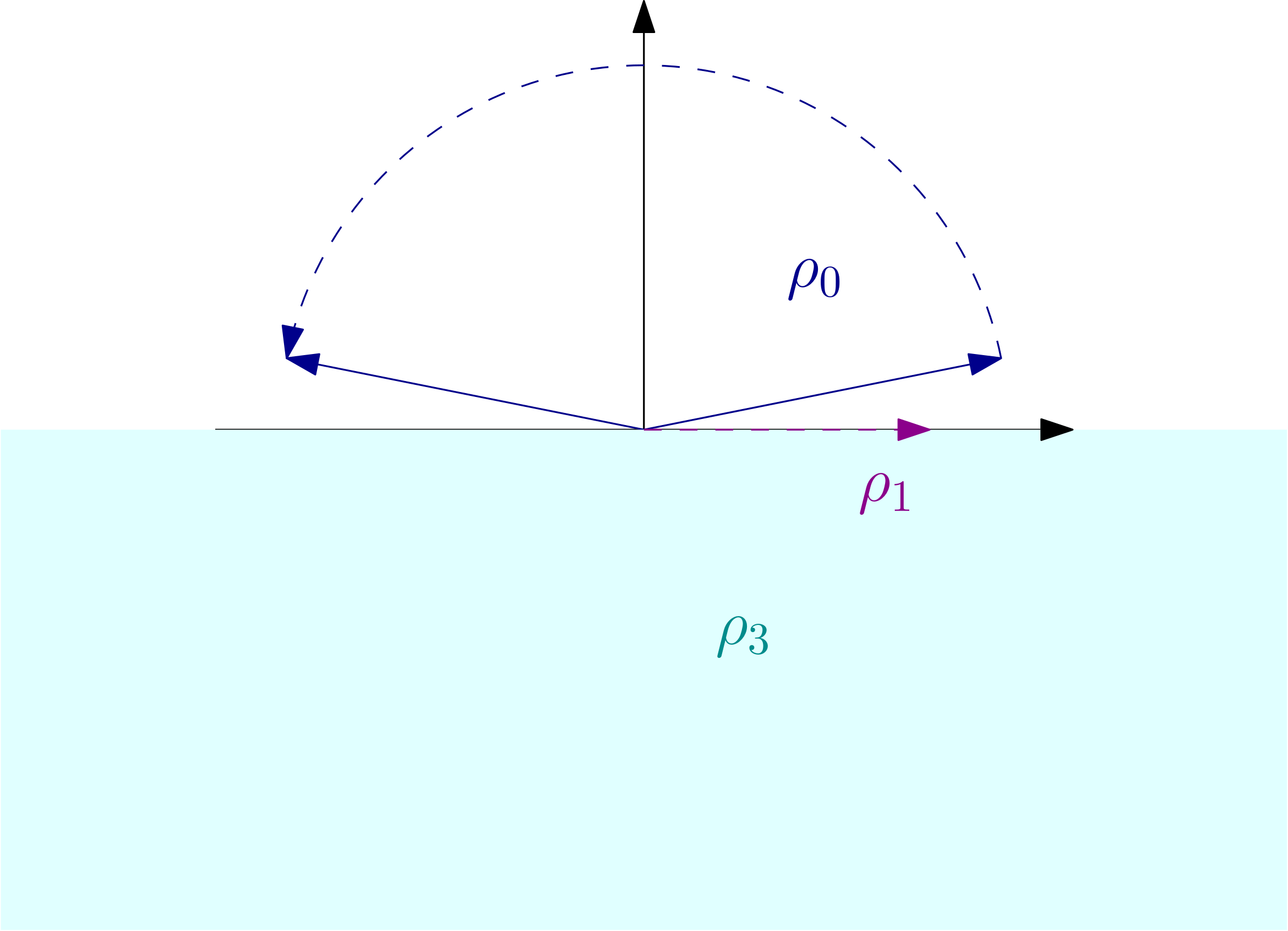
On the left, I represent the additional challenge of working with pair counting surfaces for pairs. One may increase or decrease the characteristic of the appropriate two-dimensional sheaves by adding a curve with the corresponding sign $\chi=\pm n$ in its character $(\beta,\chi)$. This necessitates the construction of a new family of stability conditions that ranges over all characteristics of one-dimensional sheaves. Such sheaves contribute to the wall-crossing between $PT^1$ and $PT^0$ stable pairs of BKP, the stability for which is represented on the right.
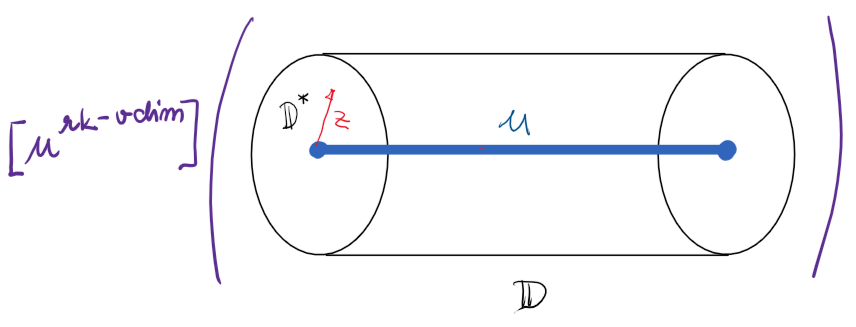

To prove the results relating the different surface counting theories, I use my families of vertex algebras explained in [Project 1](https://arkadijbojko.github.io/mypage/projects/1_project/) to extract the conjectured formulae from wall-crossing formulae between $PT^{(0)}$ and $PT^{(1)}$ stabilities. Taking the right coefficient of the family of vertex algebras in the formal variable $u$ is represented on the left. On the right, I offer a different illustration of the stability conditions interpolating between $PT^{(0)}$ and $PT^{(1)}$ stable pairs.