Project 4

K-theoretic wall-crossing for Calabi–Yau fourfolds

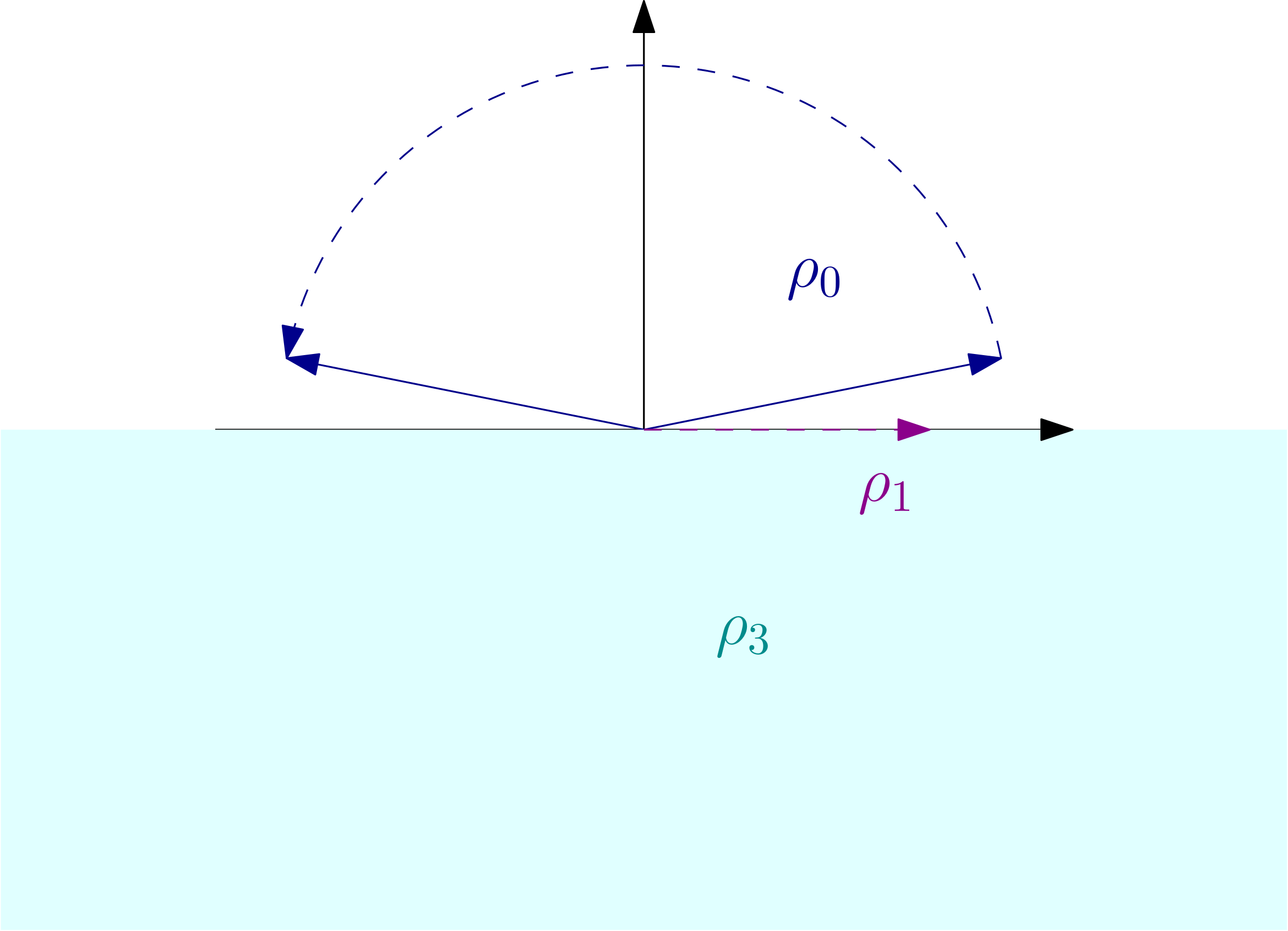
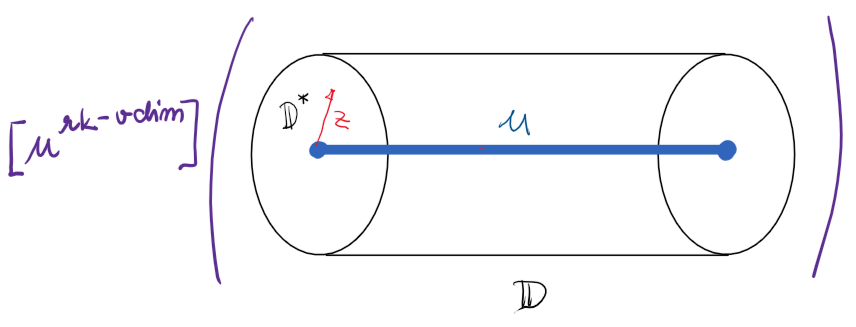
I extend my work from Project 1 and Project 3 to equivariant K-theory in collaboration with N. Kuhn, F. Thimm, and H. Liu. This will include proving the Calabi–Yau four DT/PT equivariant vertex and many K-theoretic conjectures of Bae–Kool–Park. One consequence we will obtain when working with elliptic fibrations is a new kind of K-theoretic DT/PT correspondence for Fano threefolds in terms of the symmetrized K-theoretic Euler class of the tautological $L^{[n]}$ for a line bundle $L$.

Each one of the above graphics represents an element of the fixed point locus a Hilbert scheme of curves or surfaces on a toric Calabi--Yau fourfold after projecting to the first three axes of $\CC^4$- Going from left to right the figure depicts curves along the $z_1$, $z_2$, and $z_3$ axes, curves with added points, and surfaces curves and points.

You can also put regular text between your rows of images. Say you wanted to write a little bit about your project before you posted the rest of the images. You describe how you toiled, sweated, bled for your project, and then… you reveal its glory in the next row of images.

From the point of stability conditions, nothing changes compared to Project 3, so we still work with the family of conditions portrayed on the left. The argument needed to extract closed formulae from the wall-crossing theory will be a K-theoretic refinement of my families of vertex algebras on the right. It boils down to a fitting rigidity argument, but its representation theoretic interpretation remains to be found.