Project 5
Lecture notes "Derived algebraic geometry (A guide to local models for shifted symplectic structures)"
These lecture notes are meant to give a gentle introduction to derived algebraic geometry and local models of derived stacks. They are primarily aimed at enumerative algebraic geometers, who want to understand the role of shifted symplectic structures and where these structures arise from. In the process, I prove the deformation invariance of virtual fundamental classes counting sheaves on Calabi-Yau fourfolds under the assumption that orientations exist in a family.
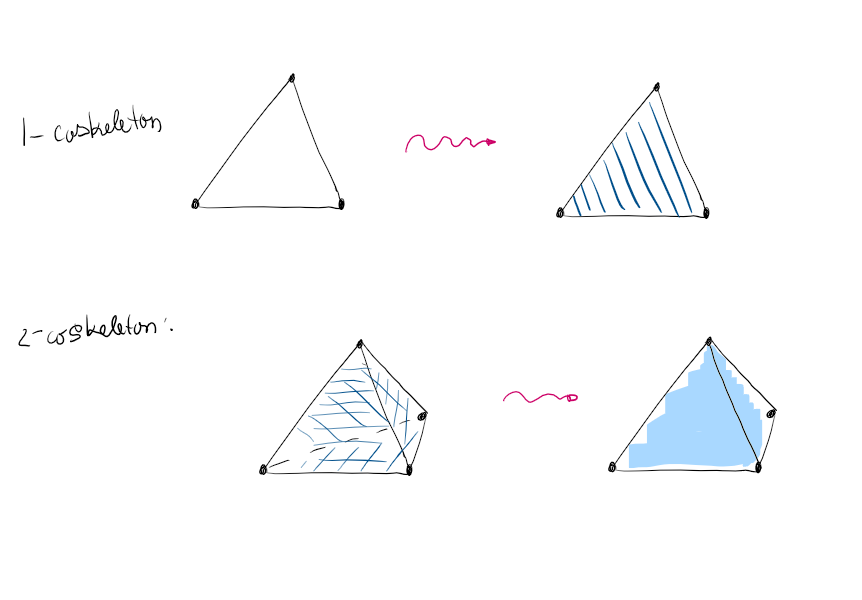
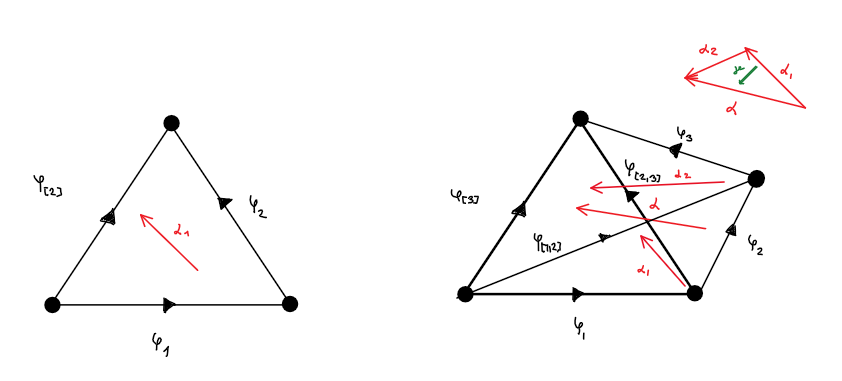
Higher algebraic geometry, of which derived algebraic geometry is a subclass, can be formulated in terms of simplicial sets. They play the role of sets or groupoids in classical algebraic geometry. To make some definitions more approachable, I sketched them using low-dimensional simplicial sets.
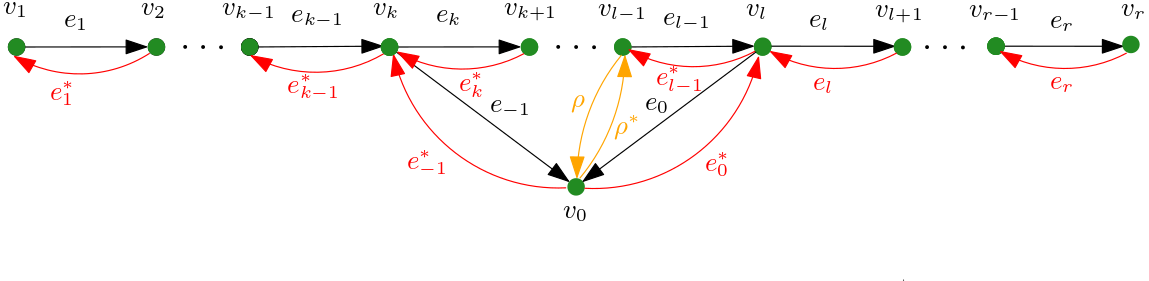
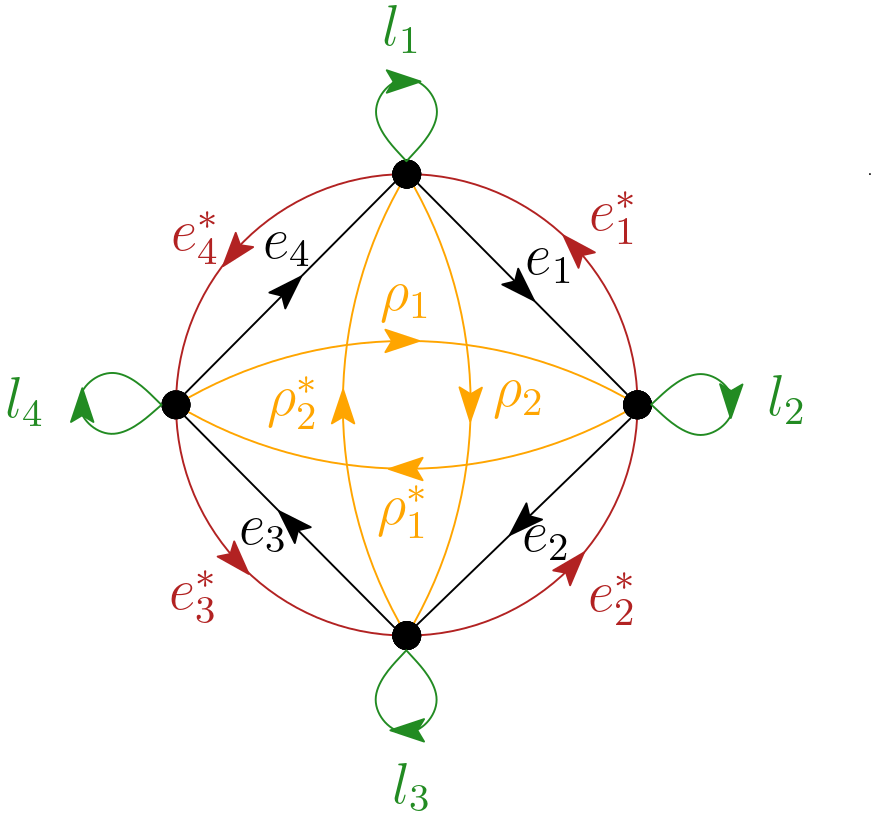
When explaining Calabi-Yau dg quivers, I presented examples from my ongoing Project 1. The first dg-quiver is a natural Calabi-Yau four completion of a quasi-smooth dg-quiver. The example on the right is much more interesting as it is truly Calabi-Yau four without an underlying quasi-smooth dg-quiver. It is the simplest such example I could come up with.