SIMIS-Sinica Interdisciplinary workshop
I have invited 6 speakers from Academia Sinica working on subjects I am interested in. To establish stronger relations between our institutes, there will also be 6 speakers from SIMIS on related topics.
Program
The workshop will take place in R610 at SIMIS from September 16 to September 19.
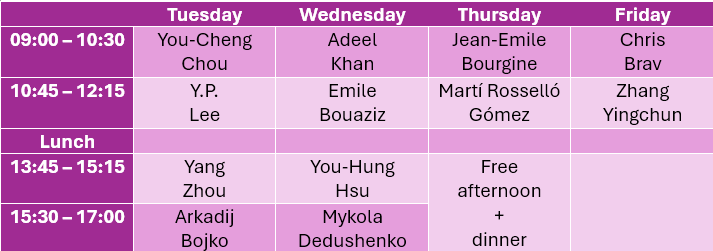
The dinner will be at 7pm at the restauran called 御延公馆·上海菜. The precise address is 黄浦区南京东路299号宏伊国际广场6层 S-601单元.
Abstracts
You-Cheng Chou
Title: Permutation equivariant quantum K-theory of a point
Abstract: In the first part, I will provide motivation for developing a K-theoretic version of Witten-Kontsevich theory. Then I will review known results about computations of (permutation equivariant) quantum K-theory of a point.
In the second part, I will explain a new approach to these computations. The approach involves a recursive pushforward technique applied to the universal cotangent line bundle and pluri-Hodge bundle. This technique is combinatorially simpler for not using the Kawasaki-Hirzebruch-Riemann-Roch theorem. As a result, we obtain a closed formula on genus 1. This is a joint work with Y.-P. Lee.
YP Lee
Title: Analytic continuation and wall-crossing in Gromov-Witten theory
Abstract: The wall-crossing in the “Kahler moduli” produces various changes of the target, including flops, flips and blowups. As was advocated almost two decades ago, these should be formulated in terms of analytic continuations of generating functions. This is based on joint work with Hui-Wen Lin and Chin-Lung Wang (National Taiwan University).
Yang Zhou
Title: Mixed-Spin-P fields and GLSM
Abstract: The theory of Mixed-Spin-P (MSP) fields was introduced by Chang-Li-Li-Liu for the quintic threefold, aiming at studying its higher-genus Gromov-Witten invariants. Chang-Guo-Li has successfully applied it to prove conjectures including the BCOV Feynman rule, Yamaguchi-Yau’s polynomiality conjecture and the Holomorphic Anomaly Equation. Meanwhile, Fan-Jarvis-Ruan introduced a mathematical theory of Gauged Linear Sigma Model (GLSM), associating a counting theory to a GIT quotient with a super-potential, under suitable assumptions.
In this talk, we first introduce a common generalization of both works, by introducing new stability conditions in the mathematical GLSM. Then we talk about some recent process on its applications. On the one hand, it gives a generalization of MSP to more target spaces. On the other hand, it also defines other interesting counting theories.
Arkadij Bojko
Title: Nekrasov’s conjecture and its generalizations via CY4 wall-crossing
Abstract: Nekrasov conjectured a closed formula for a series of invariants on the Hilbert schemes of C^4. Using wall-crossing for CY4 quivers, I aim to give a new self-contained proof of this conjecture. This method naturally includes more general cases, such as quotients of C^4 by finite groups.
Adeel Khan
Title: Virtual orbifold Grothendieck–Riemann–Roch
Abstract: For schemes, Chow homology and K-theory of coherent sheaves provide two homology theories which are closely linked by the Grothendieck-Riemann-Roch theorem. For stacks, the naive generalization of this result is false. Nevertheless, work of Vistoli, Edidin-Graham, Toën, and others shows that for a Deligne-Mumford stack X the discrepancy can be rectified by replacing the Chow groups of X by those of its inertia stack IX. In this talk, I will introduce a new conceptual perspective on this result which in particular clarifies the mysterious appearance of the inertia stack. This perspective leads to a clean and general proof of the result, as well as a virtual generalization of Kawasaki’s orbifold Riemann-Roch formula. This is based on forthcoming joint work with Charanya Ravi.
Emile Bouaziz
Title: localisation for BZ actions on stacks.
Abstract: We explain a localisation theorem for the Tate category of quasi-coherent sheaves on a stack with an action of the homotopical circle. Most of the talk will be a leisurely introduction to the geometry of group stack actions on stacks, with many simple examples.
Jean Emile Bourgine
Title: Generalized Macdonald polynomials at higher level
Abstract: Macdonald polynomials can be introduced as eigenstates of the Macdonald Hamiltonian. This operator coincides with a certain element of the quantum toroidal gl(1) algebra evaluated in the Fock representation of levels (1,0). Representations of higher levels (r,0) produce generalizations of this Hamiltonian, and their eigenstates define generalized Macdonald polynomials. In a joint work with L. Cassia and A. Stoyan [2508.19704], we extend some of the well-known formulas obtained for ordinary Macdonald polynomials to their higher level counterpart. In particular, we propose a generalization of the formula relating Macdonald polynomials to Whittaker vectors obtained by Garsia, Haiman and Tesler. The talk will start with a brief review of the quantum toroidal gl(1) algebra, and its action on the ring of symmetric functions. Then, I will introduce Macdonald polynomials and their generalizations, and present our main results. I will conclude with a discussion on possible applications to the (q,t)-deformed integrable hierarchies recently introduced with A. Garbali.
You-Hung Hsu
Title: 0-affine quantum groups as K-theoretic Hall algebras.
Abstract: Hall algebras play a central role in realizing quantum groups, beginning with Ringel’s theorem and continuing through cohomological and K-theoretic Hall algebras. In this talk, I will discuss the case of Arkhipov–Mazin’s 0-affine quantum group.
I will present a new result identifying the positive part U_n^+ of the 0-affine quantum group with the K-theoretic Hall algebra of the typeA_{n−1} quiver. Building on earlier work on shifted 0-affine algebras, I will also describe categorical U^+_n-actions on derived categories of coherent sheaves on partial flag varieties, which induce semiorthogonal decompositions of weight categories. Finally, I will also remark on some potential further directions.
Martí Rosselló Gómez
Title: The Giant Graviton Expansion for the 1/2-BPS index
Abstract: I will review the giant graviton expansion, an approach that reorganizes finite-N indices in superconformal field theories as the large-N result multiplied by systematic corrections. These corrections have a natural holographic interpretation in terms of branes in the bulk, known as giant gravitons. I will then derive the half-BPS index of N=4 SYM directly from the bulk AdS5xS5 and explain how the analytic continuation found in the literature can be understood as an instance of wall-crossing.
Mykola Dedushenko
Title: TBA
Abstract: TBA
Chris Brav
Title: The universal Grassmannian in condensed mathematics
Abstract: After a brief introduction to condensed mathematics in the sense of Clausen-Scholze, I introduce an integral form of a universal Grassmannian admitting specialisations to the algebraic Sato Grassmannian and the analytic Segal-Wilson Grassmannian, as well as non-archimedean specializations. If time permits, we speculate on applications to the arithmetic study of solutions of the KdV hierarchy. This is work in progress with Yingdi Qin.
Zhang Yingchun
Title: quantum cohomology and cluster algebra.
Abstract: In this talk, I will present our recent progress in the relation between the cluster algebra and the quantum cohomology ring. For a given quiver with potential function, there is an associated cluster algebra. At the same time, one can consider the associated varieties which is defined as the critical locus of the potential function and its “quantum cohomology ring”. We claim that the quantum cohomolog ring naturally admits a cluster algbera structure, and this holds for general quivers with potential functions in some sense.